Introducing Probability

Definitions, examples, and axioms

class date

09/28/23

In an enormously entertaining paper written about a decade ago, the economist Peter Backus estimated his chance of finding a girlfriend on any given night in London at about 1 in 285,000 or 0.0000034%. As he writes, this is either depressing or cheering news, depending on what you had estimated your chance to be before reading the paper.¹ This paper is interesting for us because it uses a probabilistic argument (originally developed by the astronomer and astrophysicist Frank Drake to estimate the probability of extra-terrestrial civilizations) to think about his dating problems. Anyone can follow the arguments put forward by Backus, including his statements that use probability.

We all have some notion of chance or probability, and can ask questions like:

What is the chance you will get an A in Stat 20? (About 32%, based on last fall.)²
What is the chance the 49ers will win the Super Bowl this year? (About 1 in 7, higher than any other team, as of September 21.)³
What is the chance you will roll a double on your next turn to get out of jail while playing Monopoly? (One in six.)
What is the chance that the next President of the United States will be Joe Biden? (A little under 40%.) ⁴

To answer such questions, we need to quantify uncertainty and randomness, and that is the focus of this new unit: Generalization.

So far, we have examined data sets and summarized them, both numerically and visually. We have looked at data distributions, and associations between variables. Can we extend the conclusions that we make about the data sets to larger populations? If we notice that bill length and flipper length have a strong linear relationship for the penguins in our data, can we say this is true about all penguins? How do we draw valid conclusions about the population our data was drawn from? These are the kinds of questions we we will study using tools from probability theory.

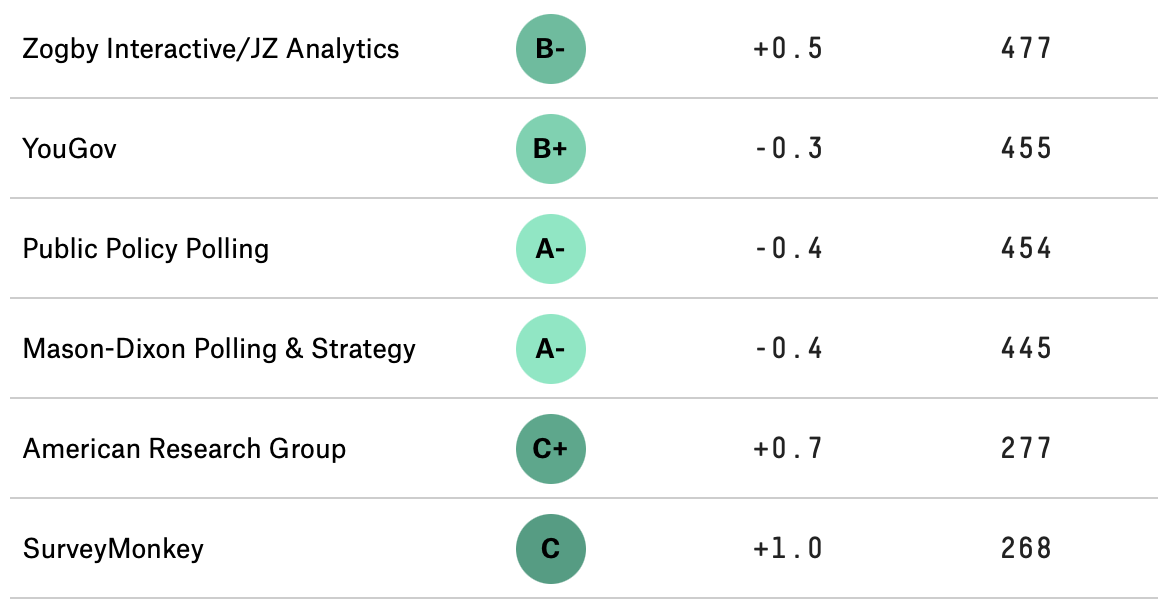
In order to be taken seriously, we need to be careful about how we collect data, and then how we generalize our findings. For example, you may have observed that some polling companies are more successful than others in their estimates and predictions, and consequently people pay more attention to them. Below is a snapshot of rankings of polling organizations from the well-known website FiveThirtyEight⁵, and one can imagine that not many take heed of the polling done by the firms with C or worse grades. According to the website, the rankings are based on the polling organization’s ``historical accuracy and methodology”.

In order to make estimates as these polling organizations are doing, or understand the results of a clinical trial, or other such questions in which we generalize from our data sample to a larger group, we have to understand the variations in data introduced by randomness in our sampling methods. Each time we poll a different group of voters, for example, we will get a different estimate of the proportion of voters that will vote for Joe Biden in the next election. To understand variation, we first have to understand how probability was used to collect the data.

Since classical probability came out of gambling games played with dice and coins, we can begin our study by thinking about those.

De Méré’s Paradox

In 17th century France, gamblers would bet on anything. In particular, they would bet on a fair six-sided die landing 6 at least once in four rolls. Antoine Gombaud, aka the Chevalier de Méré, was a gambler who also considered himself something of a mathematician. He computed the chance of a getting at least one six in four rolls as 2/3 $(4 \times (1/6) = 4/6)$. He won quite often by betting on this event, and was convinced his computation was correct. Was it?

The next popular dice game was betting on at least one double six in twenty-four rolls of a pair of dice. De Méré knew that there were 36 possible outcomes when rolling a pair of dice, and therefore the chance of a double six was 1/36. Using this he concluded that the chance of at least one double six in 24 rolls was the same as that of at least one six in four rolls, that is, 2/3 ($24 \times 1/36$). He happily bet on this event (at least one double six in 24 rolls) but to his shock, lost more often than he won! What was going on?

We will see later how to compute this probability, but for now we can estimate the value by simulating the game many times and looking at the proportion of times we see at least one six in 4 rolls of a fair die, and do the same with at least one double six in 24 rolls.

Number of simulations = 1000

  prop_wins_game_1
1            0.514

  prop_wins_game_2
1            0.487

You can see here that the poor Chevalier wasn’t as good a mathematician as he imagined himself to be, and didn’t compute the chances correctly. 🧐 You can play with this simulation in the ``Ideas in Code” section below.

Basics

Before we get going with examples, let’s establish some terminology:

Experiment: An action, involving chance, that can result in a finite number of possible outcomes (results of the experiment). For example, a coin toss is an experiment, and the possible outcomes are the coin landing heads or tails.

Outcome space: This is just a set. It is the collection of all the possible outcomes of an experiment is called an outcome space or sample space, and we denote it by the upper case Greek letter $\Omega$ (``Omega”). For example, if we toss a coin, then the corresponding outcome space is $\Omega = \{\text{Heads, Tails}\}$. If we roll a die, then the corresponding outcome space $\Omega = \{1, 2, 3, 4, 5, 6\}$. We will denote a set by enclosing the elements of the set in braces: $\{ \}$.

Event: A collection of outcomes as a result of the experiment being performed, perhaps more than once. For example, we could toss a coin twice, and consider the event of both tosses landing heads. We usually denote events by upper case letters from the beginning of the alphabet: $A, B, C, \ldots$. An event is a subset of the outcome space, and we denote this by writing $A \subset \Omega$.

Example: Tossing a fair coin

Suppose we toss a fair coin, and I ask you what is the chance of the coin landing heads. Like most people, you reply 50%. Why? Well… (you reply) there are two possible things that can happen, and if the coin is fair, then they are both equally likely, so the probability of heads is 1/2 or 50%.

Here, we have thought about an event (the coin landing heads), seen that there is one outcome in that event, and two outcomes in the outcome space, so we say the probability of the event is 1/2. We can generalize this: let’s say that there are $n$ possible outcomes in the outcome space $\Omega$, and an event $A$ has $k$ possible outcomes. If all the outcomes are equally likely to happen (as in a die roll or coin toss), then we say that the chance of $A$ is $\displaystyle \frac{k}{n}$. If we denote the probability of the event $A$ as $P(A)$, then we can say that \[ P(A) = \frac{k}{n} \]

For a fair coin, we can say $P(\text{Heads}) = \displaystyle \frac{1}{2}$.

Equally likely outcomes: When all the possible outcomes in a finite outcome space of size $n$ happen with the same probability, which is $\displaystyle \frac{1}{n}$. To find the probability of an event $A$, just count how many outcomes are in $A$ and divide that by $n$.

Example: Tossing a fair six-sided die⁶

Consider rolling a fair six-sided die: six outcomes are possible so $\Omega = \{1, 2, 3, 4, 5, 6\}$. Since the die is fair, each outcome is equally likely, with probability $= \displaystyle \frac{1}{6}$. We can list the outcomes and their probabilities in a table.

Outcome	$1$	$2$	$3$	$4$	$5$	$6$
Probability	$\displaystyle \frac{1}{6}$	$\displaystyle \frac{1}{6}$	$\displaystyle \frac{1}{6}$	$\displaystyle \frac{1}{6}$	$\displaystyle \frac{1}{6}$	$\displaystyle \frac{1}{6}$

In order to compute the probabilities of events, we need to set some rules.

Axioms of probability

The probability (or chance - we use these words interchangebly) of an event needs to satisfy some basic mathematical rules called axioms (which are intuitively clear if you think of the probability of an event as the proportion of the outcomes that are in it). There are three basic rules that will help us compute probabilities:

Rule 1: The chance of any event is at least $0$: $P(A) \ge 0$ for any event $A$.
Rule 2: The chance of an outcome being in $\Omega$ is $1$: $P(\Omega) = 1$. This is true because we can consider that the probability of $\Omega$ is the number of outcomes in $\Omega$ divided by $n$, which is $n/n = 1$.

Before we write the third rule, we need some more definitions and notation:

Impossible event: An event with no outcomes in it. Denoted by either empty braces $\{\}$ or the symbol for the empty set $\emptyset$. The probability of the impossible event is $0$.

Union of events: Given events $A$, $B$, we can define a new event called $A$ or $B$, which consists of all the outcomes that are either in $A$ or in $B$ or in both. This is also written as $A \cup B$, read as ``$A$ union $B$’’.

Intersection of events: Given events $A$, $B$, we can define a new event called $A$ and $B$, which consists of all the outcomes that are both in $A$ and in $B$. This is also written as $A \cap B$, read as ``$A$ intersect $B$’’.

Now we consider events that don’t intersect or overlap at all, that is, they are disjoint from each other, or mutually exclusive:

Mutually exclusive events: If two events $A$ and $B$ do not overlap, that is, they have no outcomes in common, we say that the events are mutually exclusive. Note that if $A$ and $B$ are mutually exclusive, then we know that if one of them happens, the other one cannot. We denote this by writing $A \cap B = \emptyset$ and read this as $A$ intersect $B$ is empty. Therefore, we have that $P(A \cap B) = P(\emptyset) = 0$.

For example, if we are playing De Méré’s second game, the event that we roll a pair of sixes and the event that we roll a pair of twos cannot happen on the same roll. These are mutually exclusive. Another example: the events that President Biden is re-elected and the event that Donald Trump is elected as President cannot both happen, therefore they are mutually exclusive events.

More examples:

If we roll a die, the events that we roll an even number and the event that we roll an odd number are mutually exclusive, but the events that we roll an even number and the event that we roll a prime number are not mutually exclusive, since the number 2 is both even and prime.

The event that Manchester City wins the English Premier League (EPL) in 2024, and the event that Arsenal wins the EPL in 2024 are mutually exclusive, but the events that Manchester City are EPL champions in 2024 and Manchester City are EPL champions in 2023 are not mutually exclusive.

Now for the third axiom:

Rule 3: If $A$ and $B$ are mutually exclusive ($A \cap B = \emptyset$), then $P(A \cup B) = P(A) + P(B)$. That is, for two mutually exclusive events, the probability that either of the two events might occur is the sum of their probabilities. This is called the addition rule.

Example:

For example, consider rolling a fair six-sided die, and the two events $A$ and $B$, where $A$ is the event of rolling a multiple of $5$, and $B$ is the event that we roll a multiple of $2$.

The only outcome in $A$ is $\{5\}$, while $B$ consists of $\{2, 4, 6\}$. $P(A) = 1/6$, and $P(B) = 3/6$. Since $A \cap B =\emptyset$, that is, $A$ and $B$ have no outcomes in common, $P(A \cup B) = P(A) + P(B) = 1/6 + 3/6 = 4/6$.

An important consequence of rule 3 is the complement rule below. First, we need a definition.

Complement of a set $A$: Let $A$ be an event in $\Omega$. The complement of $A$, written as $A^C$ consists of all those outcomes in $\Omega$ that are not in $A$.

The complement rule: $P(A) + P(A^C) = 1$ (since $A \cup A^C = \Omega$)

Example of using the rules

Penguins

Consider the penguins data, which has 344 observations, of which 152 are Adelie penguins and 68 are Chinstrap penguins. Suppose we pick a penguin at random, what is the probability that we would pick an Adelie penguin? What about a Gentoo penguin?

Check your answer

Let $A$ be the event of picking an Adelie penguin, $C$ be the event of picking a Chinstrap penguin, and $G$ be the event of picking a Gentoo penguin. Assuming that all the penguins are equally likely to be picked, we see that then $P(A) = 152/344$, and $P(C) = 68/344$. Since only one penguin is picked, we see that $A, C$, and $G$ are mutually exclusive. This means that $P(A)+P(C)+P(G) = 1$, since $A, C$, and $G$ together make up all of $\Omega$. Therefore the complement of $G$ which is a penguin that is not Gentoo consists of Adelie and Chinstrop penguins, and $P(G^C) = P(A \cup C) = P(A) + P(C) = (152+68)/344 = 220/344$ (addition rule).

Finally, the complement rule tells us that $P(G) = 1 - P(G^C) = 1 - 220/344 = 124/344$.

WARNING!!

We use $A$ to denote an event or a set, while P(A) is a number - you can think of $P(A)$ as representing the relative size of $A$. This means that the following types of statements don’t make sense as we haven’t defined what it means to add sets or union numbers etc.:

$P(A) \cup P(B)$ or $P(A) \cap P(B)$
$A + B$, or $A - B$, or $A \times B$ etc

Venn Diagrams

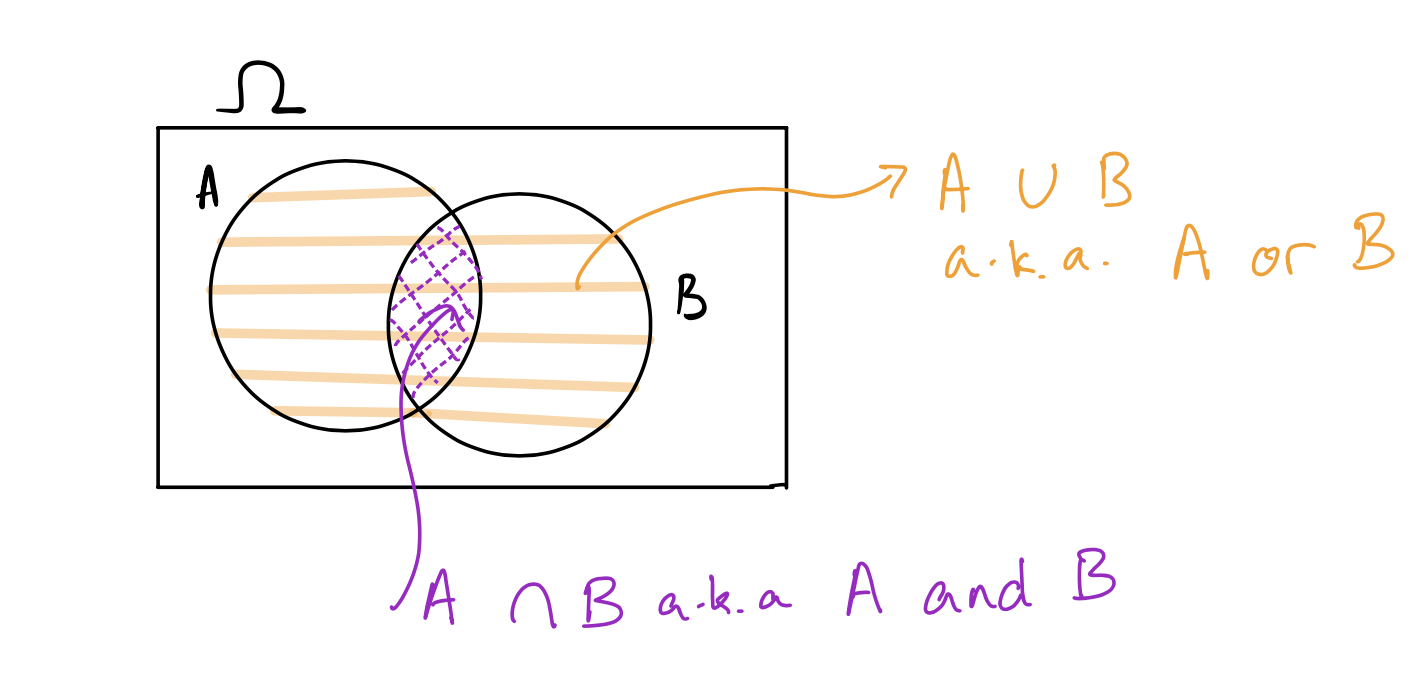
We often represent events using Venn diagrams. The outcome space $\Omega$ is usually represented as a rectangle, and events are represented as circles inside $\Omega$. Here is a Venn diagram showing two events $A$ and $B$, their intersection, and their union:

Here is a Venn diagram showing two mutually exclusive events (no overlap):

Examples

1. Tossing a fair coin

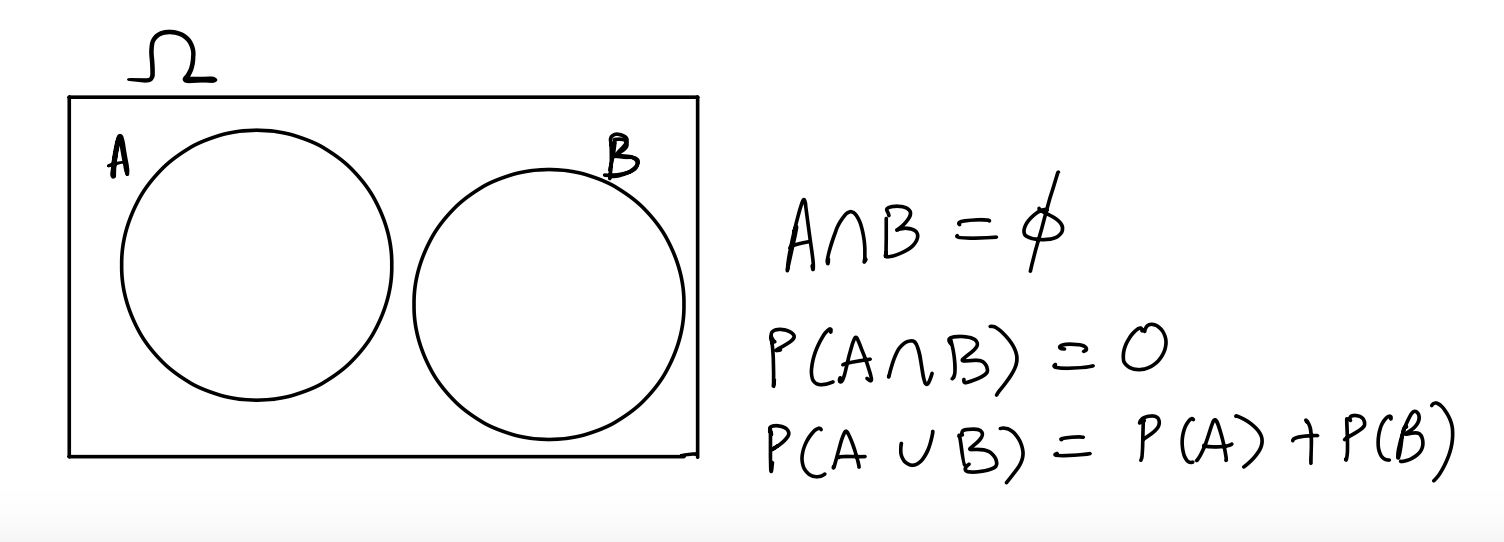
Suppose we toss a coin twice and record the equally likely outcomes. What is $\Omega$? What is the chance of at least one head?

Solution: $\Omega = \{HH, HT, TH, TT\}$, where $H$ represents the coin landing heads, and $T$ represents the coin landing tails. Note that since we can get exactly one head and one tail in two ways, we have to write out both ways so that all the outcomes are equally likely.

Now, let $A$ be the event of getting at least one head in two tosses. We can do this by listing the outcomes in $A$: $A = \{HH, HT, TH\}$ and so $P(A) = 3/4$.

Alternatively, we can consider $A^C$ which is the event of no heads, so $A^C = \{TT\}$ and $P(A^C) = 1/4$.

In this case, $P(A) = 1- P(A^C) = 1-1/4 = 3/4$.

Now you try: Let $\Omega$ be the outcome space of tossing a coin three times. What is the probability of at least one head? What about exactly one head?

Check your answer

$\Omega = \{HHH, HHT, HTH, THH, HTT, THT, TTH, TTT \}$.

Let $A$ be the event of at least one head. Then $A^C$ is the event of no heads, so $A^C = \{TTT\}$, and $P(A^C) = 1/8$. Therefore $P(A) = 1-1/8 = 7/8$. Note that this is much quicker than listing and counting the outcomes in $A$.

If $B$ is the event of exactly one head, then $B = \{HTT, THT, TTH\}$ and $P(B) = 3/8$.

2. A box of tickets

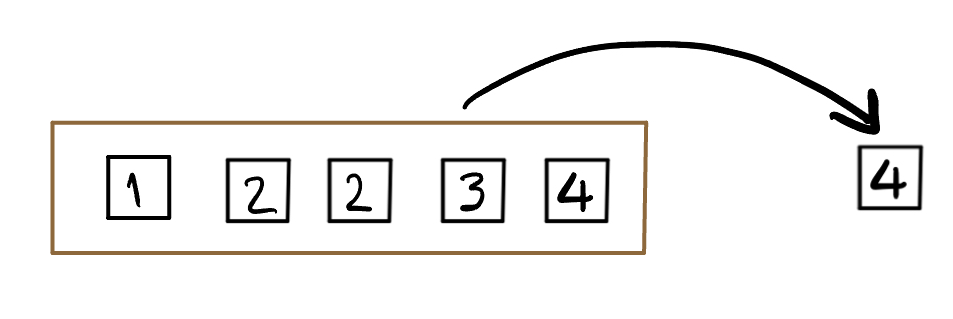
Consider the box above which has five almost identical tickets. The only difference is the value written on them. Imagine that we shake the box to mix the tickets up, and then draw one ticket without looking so that all the tickets are equally likely to be drawn⁷.

What is the chance of drawing an even number?

Check your answer

Solution:

Let $A$ be the event of drawing an even number, then $A = \{2, 2, 4\}$: we list 2 twice because there are two tickets marked 2, making it twice as likely as any other number. $P(A) = 3/5$

Probability distributions vs empirical distributions

The plots of distributions that we have seen so far have been visualizations of data, and so are called empirical distributions. We can represent the theoretical probabilities visually with bars, and we call this a probability distribution. Note that we do not need to collect data for this type of graph.

Here is a plot of the probability distribution of the value of the drawn ticket. It is a visual representation of the table we drew earlier, and you can see that the bar over 2 is twice as tall. This is because there are twice as many tickets marked 2 as any other numbers.

Code

tkts_box <- c(1, 2, 3, 4)
prob_box <- c(1/5, 2/5, 1/5, 1/5)

box <- c(1, 2, 2, 3, 4)

p1 <- data.frame(box) %>% 
  ggplot(aes(x=box)) +
  geom_bar(width = 0.98, fill = "darkorchid") +
  xlab("ticket value")  +
  ggtitle("Ticket distribution")

p2 <- data.frame(tkts_box) %>% 
  ggplot(aes(x=tkts_box, y=prob_box)) +
  geom_col(width = 0.98, fill = "goldenrod2") +
  xlab("ticket value") +
  ylab("probability")

p1+p2

Notice that the only difference between these two plots is the vertical scale. When the tickets are equally likely, the box distribution (the purple plot) completely determines the probability distribution (the golden plot).

How about if we draw 50 times at random with replacement from this box (that is, each time we draw a ticket, we put the ticket back before we draw another ticket, so that the box we draw from always has the same number of tickets), and see what our sample looks like. That is, we will see what proportion of the draws are 1’s, 2’s etc.

Code

set.seed(12345)
box <- c(1,2,2,3,4)
sample_size <- 50
sample_box <- sample(box, size = sample_size, replace = TRUE)
data.frame(sample_box) %>%
  ggplot(aes(sample_box)) + 
  geom_bar(aes(y = ..prop..), width = 0.98, fill = "blue") +
  xlab("values of draws") + 
  ylab("proportion of draws")

We can see that the (blue) sample proportions look similar to the (gold) population (box) proportions (the probability distribution above), but are somewhat different. It turns out that the counts of the drawn tickets are:

Ticket	Number of times drawn	Proportion of times drawn
$\fbox{1}$	10	0.2
$\fbox{2}$	24	0.48
$\fbox{3}$	10	0.2
$\fbox{4}$	6	0.12

What we have seen here is how when we draw at random, we get a sample that resembles the population, that is, a representative sample. This is a plot of the empirical distribution, that is, a distribution that is obtained from data.

3. Tossing a biased coin

Suppose I have a coin that is twice as likely to land heads as it is to land tails. This means that I cannot represent $\Omega$ as $\{H, T\}$ since heads and tails are not equally likely. How should I write $\Omega$ so that the outcomes are equally likely?

Solution:

In this case, we want to represent equally likely outcomes, and want $H$ to be twice as likely as $T$. We can therefore represent $\Omega$ as $\{H, H, T \}$. Now the chance of the coin landing $H$ can be written as $P(A)$ where $A$ is the event the coin lands $H$ is given by 2/3.

Suppose we toss the coin twice. How would we list the outcomes so that they are equally likely? Now we have to be careful, and think about all the things that can happen on the second toss if we have $H$ on the first toss.

This is much easier to imagine if we imagine drawing twice from a box of tickets, but putting the first ticket back before drawing the second (to represent the fact that the probabilities of landing $H$ or $T$ stay the same on the second toss.)

Now, imagine the box of tickets that represents $\Omega$ to be $\fbox{H, H, T}$. We draw one ticket at first, which could be one of three tickets (there are two tickets that could be $H$, and one $T$). We can represent it using the following picture:

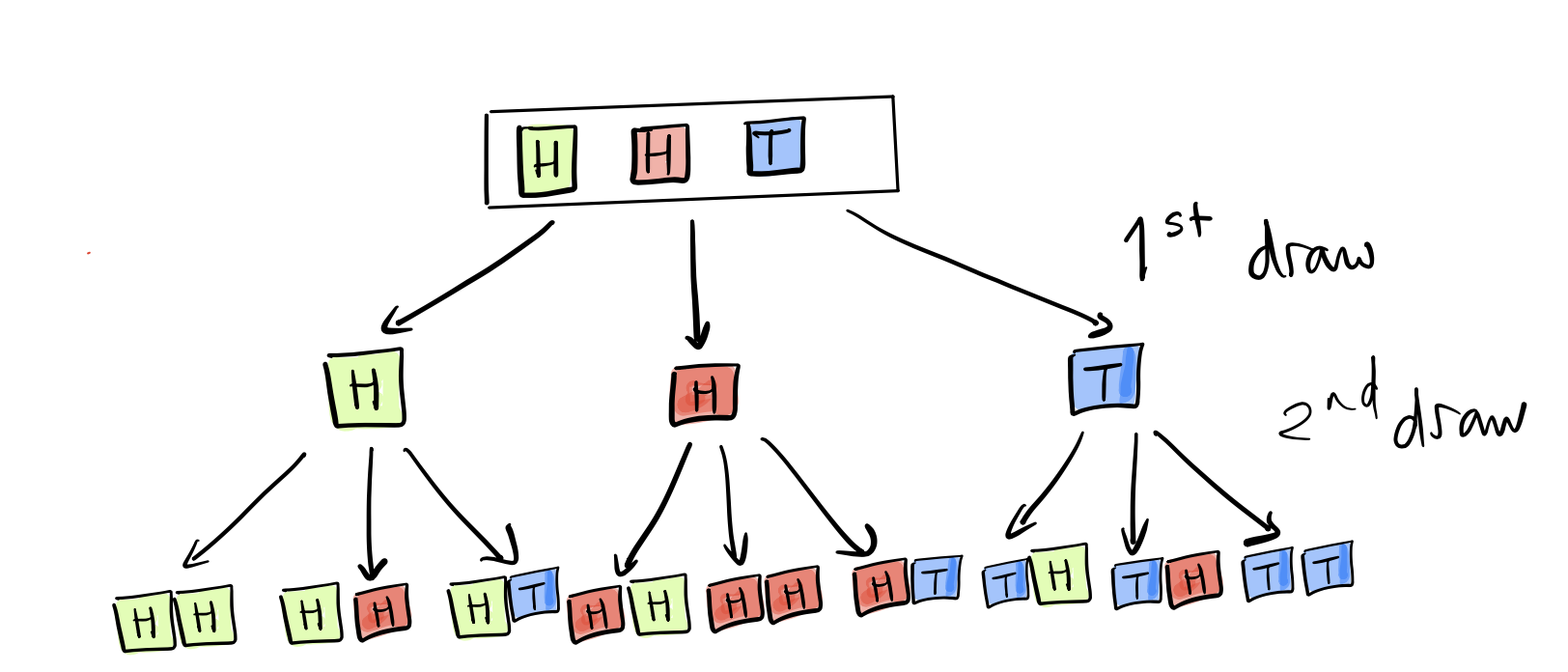
From this picture, where we use color to distinguish the two different outcomes of heads and one outcome of tails, we can see that there are 9 possible outcomes that are equally likely, and we get the following probabilities (where $HT$, for example, represents the event that the first toss is heads, followed by the second toss being tails.)

$P(HH) = 4/9,\; P(HT) = P(TH) = 2/9, P(TT) = 1/9$ (Check that the probabilities sum to 1!)

Ask yourself

What box would we use if the coin is not a fair coin, but lands heads $5$ out of $6$ times?

4. Betting on red in roulette

⁸

Expand to read this example

An American roulette wheel has 38 pockets, of which 18 are red, 18 black, and 2 are green. The wheel is spun, and a small ball is thrown on the wheel so that it is equally likely to land in any of the 38 pockets. Players bet on which colored or numbered pocket the ball will come to rest in. If you bet one dollar that the ball will land on red, and it does, you get your dollar back, and you win one more dollar, so your net gain is $1. If it doesn’t, and lands on a black or green number, you lose your dollar, and your net “gain” is -$1.

What is the chance that we will win one dollar on a single spin of the wheel?

Hint Write out the chance of the ball landing in a red pocket, and not landing in a red pocket.

Simulations

Code along

As you read through these notes, keep RStudio open in another window to code along at the console.

Drawing from a box of tickets is easily simulated in R, since there is a convenient function that does exactly what we need: draw tickets from a “box” (a vector). We will use the function sample(x, size = n, replace = FALSE), where x is the vector you want to sample from, size is the number of draws (with the default value being the length of x), and replace specifies whether the draws are with or without replacement. The default in sample() is to draw without replacement. (Note: The set.seed() function below ensures that we will get the same random sample each time we run the code.)⁹

Let’s simulate rolling a die and counting how many times we see each face.

If we roll it 6 times, we don’t really expect to see each face exactly once, and as you can see below, in this particular instance of rolling the die six times, we didn’t see the face with one spot, but saw two spots twice.

Code

set.seed(12345)
die <- 1:6

die_rolls <- sample(die, 6, replace = TRUE)

data.frame(die_rolls) %>%
  group_by(die_rolls) %>% 
  summarise(n = n())

# A tibble: 5 × 2
  die_rolls     n
      <int> <int>
1         2     2
2         3     1
3         4     1
4         5     1
5         6     1

What about if we roll the die 60 times? We should see each face about ten times:

Code

set.seed(12345)

die_rolls <- sample(die, 60, replace = TRUE)

data.frame(die_rolls) %>%
  group_by(die_rolls) %>% 
  summarise(n = n())

# A tibble: 6 × 2
  die_rolls     n
      <int> <int>
1         1    10
2         2    11
3         3    13
4         4    10
5         5     6
6         6    10

Not so great, but let’s try rolling the die 600 times:

Code

set.seed(12345)

die_rolls <- sample(die, 600, replace = TRUE)

data.frame(die_rolls) %>%
  group_by(die_rolls) %>% 
  summarise(n = n())

# A tibble: 6 × 2
  die_rolls     n
      <int> <int>
1         1   114
2         2   112
3         3   101
4         4    95
5         5    98
6         6    80

It might be better to visualize it. We will draw the probability distribution in gold, which shows the probabilities of each possible outcome (the probability distribution), and compare it to the empirical distributions in blue (plotting the data distribution, not the probability distribution) of the results of rolling the die $60, 600$, and $6000$ times. Note that the probability distribution is theoretical, where the area of the bars represent probabilities, and the total area of the bars is $1$.

Code

prob_die <- rep(1/6, 6)
set.seed(12345)

p1 <- data.frame(die) %>% 
  ggplot(aes(x = factor(die), y=prob_die)) +
  geom_col(width = 0.98, fill = "goldenrod2") +
  xlab("number of spots") +
  ylab("probability") +
  ggtitle("Probability distribution of the \n outcome of a die roll") +
  lims(y = c(0, .35))

roll_60 <- sample(die, 60, replace = TRUE)
roll_60 <- data.frame(table(roll_60)) %>% 
  mutate(prop_rolls = Freq/60)


p2 <- roll_60 %>%
  ggplot(aes(x = factor(die), y= prop_rolls)) +
  geom_col(width = 0.98, fill = "blue") +
  xlab("number of spots") +
  ylab("proportion of rolls") +
  ggtitle("Empirical distribution for \n 60 rolls") +
  lims(y = c(0, .35))


roll_600 <- sample(die, 600, replace = TRUE)

roll_600 <- data.frame(table(roll_600)) %>%
    mutate(prop_rolls = Freq/600)

p3 <- roll_600 %>%
  ggplot(aes(x = factor(die), y= prop_rolls)) +
  geom_col(width = 0.98, fill = "blue") +
  xlab("number of spots") +
  ylab("proportion of rolls") +
  ggtitle("Empirical distribution for \n 600 rolls") +
  lims(y = c(0, .35))
  

roll_6000 <- sample(die, 6000, replace = TRUE)

roll_6000 <- data.frame(table(roll_6000)) %>%
    mutate(prop_rolls = Freq/6000)


p4 <- data.frame(roll_6000) %>%
  ggplot(aes(x = factor(die), y=prop_rolls)) +
  geom_col(width = 0.98, fill = "blue") +
  xlab("number of spots") +
  ylab("proportion of rolls") +
  ggtitle("Empirical distribution for \n 6000 rolls") +
  lims(y = c(0, .35))

(p1 + p2)/(p3+p4)

The important takeaway here is that we have a theoretical probability distribution of the outcomes, and we have what actually happens when we perform the experiment over and over. Eventually, the empirical distribution begins to look like the theoretical distribution.

set.seed(12345)
box <- c(1, 2, 2, 3, 4)
sample(box,1)

[1] 2

We can use sample() to estimate the chance of a particular outcome when we aren’t sure of what that chance might be. We would do this by repeatedly sampling from the “box” with replacement (many times), then computing the proportion of times we drew each ticket. For example, say we consider our first example (the simple box), and want to estimate the chance of each ticket.

In the code below, another new function is introduced: replicate(). The function replicate(reps, expr) is a very useful function that takes as input an expression expr and evaluates it reps times, returning a vector.

box <- c(1, 2, 2, 3, 4)
draws <- replicate(2000, sample(box, 1, replace = TRUE))
ggplot(data.frame(draws), aes(x=draws)) + 
  geom_bar(aes(y=..prop..), fill="blue", width = 0.98) + 
  ylab("proportion of draws") + 
  xlab("ticket drawn")

We see that the estimated chance of drawing a $\fbox{2}$ is about 0.4, and this is about twice the estimated chance of drawing any other ticket. Of course, we knew this already, without needing to code it in R. Let’s think of a more complicated situation:

What if we wanted to wanted to draw five tickets with replacement from this box, and sum the draws? What would be the possible values that we would get? What could their chances be? We can visualize this in R:

Code

box <- c(1, 2, 2, 3, 4)
draws <- replicate(5000, sum(sample(box, size = 5, replace = TRUE)))
ggplot(data.frame(draws), aes(x=draws)) + 
  geom_bar(aes(y=..prop..), fill="blue", width = 0.98) + 
  ylab("proportion") + 
  xlab("sum of draws") + 
  scale_x_continuous(breaks = seq(min(draws), max(draws), by = 1))

We can see that there is a lot more variation in the values taken by the sum of 5 draws.

Tossing a fair coin

We can estimate the chances of various outcomes related to coin tossing, using sampling from a box.

Suppose, for example, that we would like to figure out the chance of exactly 2 heads if we toss a coin 4 times. Think about how you would use the functions sample() and replicate() to model this, using the 0-1 box we defined earlier, for tossing a coin.

Code

coin <- c(0, 1) #1 represents the toss landing heads
two_heads <-replicate(50000, sum(sample(coin, 4, replace = TRUE)) == 2)
cat("The proportion of times we see 2 heads out of 4 tosses is", mean(two_heads))

The proportion of times we see 2 heads out of 4 tosses is 0.38054

Rolling a pair of dice and summing the spots

This is something that we could use if we wanted to play Monopoly and couldn’t find the dice. Recall the box we used to simulate a die roll. Now we are going to define a vector in R to represent a die, and sample twice with replacement, from this vector, and add the spots.

Code

die <- 1:6
# to simulate rolling a die twice and summing the spots
draws <- sample(die, size = 2, replace = TRUE)
sum(draws)

[1] 6

We could also repeat it many times and estimate the chance of each of the possible outcomes.

Code

many_draws <- replicate(5000, sum(sample(die, size = 2, replace = TRUE)))
ggplot(data.frame(many_draws), aes(x=many_draws)) + 
  geom_bar(aes(y=..prop..), fill="blue", width = 0.98) + 
  ylab("proportion") + 
  xlab("sum of two draws") + 
  scale_x_continuous(breaks = seq(min(many_draws), 
                                  max(many_draws), by = 1))

Ask yourself

We know all the possible outcomes of summing a pair of dice (between $2$ and $12$ spots). Why not make a box with tickets labeled $2, 3, 4, \ldots, 12$ and draw once from that box? If we did indeed want a box from which we would only draw once, what would the box be? (Hint: How many possible outcomes would there be if you rolled a pair of dice. )

Summary

In this lecture, we introduced equally likely outcomes,and defined the outcome space of an experiment.
Then, using equally likely outcomes, we defined the probability of an event as the ratio of the number of outcomes in the event to the number of total outcomes in the outcome space.
We wrote down the rules of probability, after defining unions, intersections, and mutually exclusive events and Venn diagrams
We saw how to simulate probabilities using sample() and replicate()

Materials from class

Slides

Ideas in Code

You can run the simulations yourself using the code below. Copy and paste it into RStudio and play around with it.

First, lets define two vectors called die and pair_of_dice that represent the outcome spaces of rolling a die once and rolling a pair of dice once, respectively.

die <- 1:6

die

[1] 1 2 3 4 5 6

pair_dice <- c( 2, 3, 3, rep(4,3), rep(5,4), rep(6, 5), rep(7,6), 
                rep(8,5), rep(9,4), rep(10,3), rep(11,2), 12)

pair_dice

 [1]  2  3  3  4  4  4  5  5  5  5  6  6  6  6  6  7  7  7  7  7  7  8  8  8  8
[26]  8  9  9  9  9 10 10 10 11 11 12

We used a new function here called rep(x, n). This function has two arguments, the first x is a vector of any type, and the second n is an integer. It returns an object creates a vector of the same type asx by repeating x, n times. For examplerep(2,5) gives 2, 2, 2, 2, 2, rep(2:4,5) gives 2, 3, 4, 2, 3, 4, 2, 3, 4, 2, 3, 4, 2, 3, 4.

Now let’s set up the first game, and repeat it 1000 times. You can change the number of simulations below. The first line has another new function called $\texttt{set.seed()}$. We write this with an integer argument that can be any integer you like, this integer is called the seed. Using this function ensures that any time you are using a random number generator (which you do when you sample at random), you will be able to reproduce your results as long as you use the same seed.

##### de mere first game ############

set.seed(123123) 
# This ensures that each time we run this code, we will get the same results.

num_simulations <- 1000 
# specifying the number of simulations, or the number of times we will play

# now we will play the game of rolling the die 4 times num_simulations times
die_4 <- replicate(num_simulations, sample(die, 4, replace = TRUE)) 

# the results of play are saved as a numerical array (a matrix), not a data frame
# so we save it as a data frame, and transpose the rows and columns so each row is the 
# result of one game
die_4_df <- data.frame(t(die_4))

# the next two lines of code are to make our data frame look better
# and you can ignore them

colnames(die_4_df) <- paste("roll", sep = " ", 1:4) 

rownames(die_4_df) <- paste("simulation", sep = " ", 1:num_simulations)

# let's take a look at our data frame
head(die_4_df)

             roll 1 roll 2 roll 3 roll 4
simulation 1      3      4      3      1
simulation 2      5      4      6      3
simulation 3      1      3      5      5
simulation 4      3      4      6      5
simulation 5      1      6      5      2
simulation 6      1      2      3      6

# we will create a new column that checks, for each play (each row), if there is at least 
# one 6. What will be the values in this column? Break the pipe and check!
# Finally, we will compute the proportion of plays in which at least one 6 was rolled.
die_4_df %>% 
  mutate(at_least_one_six = if_any(everything(), ~ . == 6)) %>%
  summarise(prop_wins = mean(at_least_one_six))

  prop_wins
1     0.512

Let’s repeat the simulation for the second game, in which we roll a pair of dice 24 times and record a win if at least one double six is rolled.

Note that the number of simulations is defined above.

set.seed(123123)

######## de mere second game  ############

# define the outcome space from rolling a pair of dice listing all the outcomes, repeated
# the number of ways that can occur. For example we can get 3 by rolling a 2, 1 or a 1, 2
# note that we can get 12 in exactly 1 way, by rolling a double six.


pair_dice <- c( 2, 3, 3, rep(4,3), rep(5,4), rep(6, 5), rep(7,6), 
                rep(8,5), rep(9,4), rep(10,3), rep(11,2), 12)

## note, not ideal because if see 7 don't know how we got it

# play the game on repeat
dice_24 <- replicate(num_simulations, sample(pair_dice, 24, replace = TRUE) )

# make a data frame
dice_24_df <-  data.frame(t(dice_24)) 

# make the data frame easier to read
colnames(dice_24_df) <- paste("roll", sep = " ", 1:24)
rownames(dice_24_df) <- paste("simulation", sep = " ", 1:num_simulations)


#head(dice_24_df)

dice_24_df %>% 
  mutate(at_least_one_boxcars = if_any(everything(), ~ . == 12)) %>%
  summarise(prop_wins_game_2 = mean(at_least_one_boxcars))

  prop_wins_game_2
1            0.478

Footnotes

Paper is at https://www.astro.sunysb.edu/fwalter/AST248/why_i_dont_have_a_girlfriend.pdf and a talk by Backus at https://www.youtube.com/watch?v=ClPPSry8bBw ↩︎
https://berkeleytime.com/grades/0-7077-all-all&1-7077-fall-2022-all ↩︎
https://www.foxsports.com/articles/nfl/2023-24-san-francisco-49ers-odds-odds-to-win-super-bowl-nfl-playoffs-division ↩︎
https://www.thelines.com/odds/election/↩︎
This website was begun as poll aggregation site, by the statistician Nate Silver.↩︎
The singular is die and the plural is dice. If we use the word “die” without any qualifiers, we will mean a fair, six-sided die.↩︎
We call the tickets equally likely when each ticket has the same chance of being drawn. That is, if there are $n$ tickets in the box, each has a chance of $1/n$ to be drawn. We also refer to this as drawing a ticket uniformly at random, because the chance of drawing the tickets are the same, or uniform.↩︎
Photo via unsplash.com↩︎
The random number generator in R is called a “Pseudo Random Number Generator”, because the process can be controlled by a “seed”. These are algorithmic random number generators, which means that if you provide the same seed (a starting number), R will generate the same sequence of random numbers. This makes it easier to debug your code, and reproduce your results if needed.↩︎

De Méré’s Paradox

Basics

Example: Tossing a fair coin

Example: Tossing a fair six-sided die6

Axioms of probability

Example of using the rules

Penguins

Venn Diagrams

Examples

1. Tossing a fair coin

2. A box of tickets

Probability distributions vs empirical distributions

3. Tossing a biased coin

4. Betting on red in roulette

Simulations

Tossing a fair coin

Rolling a pair of dice and summing the spots

Summary

Materials from class

Slides

Ideas in Code

Footnotes

Example: Tossing a fair six-sided die⁶