01:00
Hypothesis Tests II
Agenda
- Announcements
- Concept Questions
- Break
- PS 14: Hypothesis Tests II
Announcements
- RQ: Wrong By Design due Wed/Thu night at 11:59pm
- Quiz 3 is in the first half of class on Thursday/Friday.
- Problem Set 14 is due the Tuesday after break.
Concept Questions
Which pair of plots would have the greatest chi-squared distance between them? (consider one of them the “observed” and the other the “expected”)
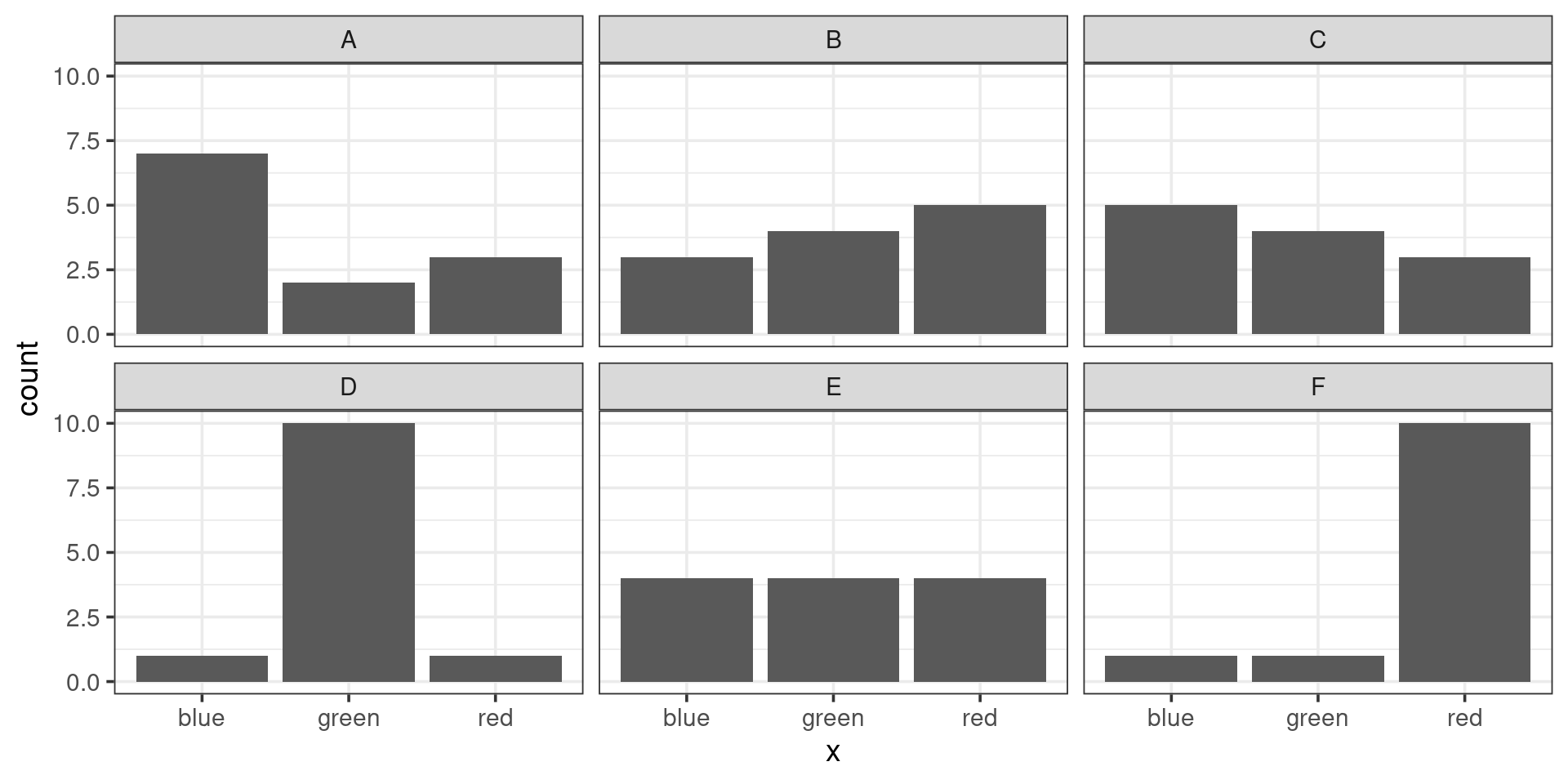
Chi-squareds Compared
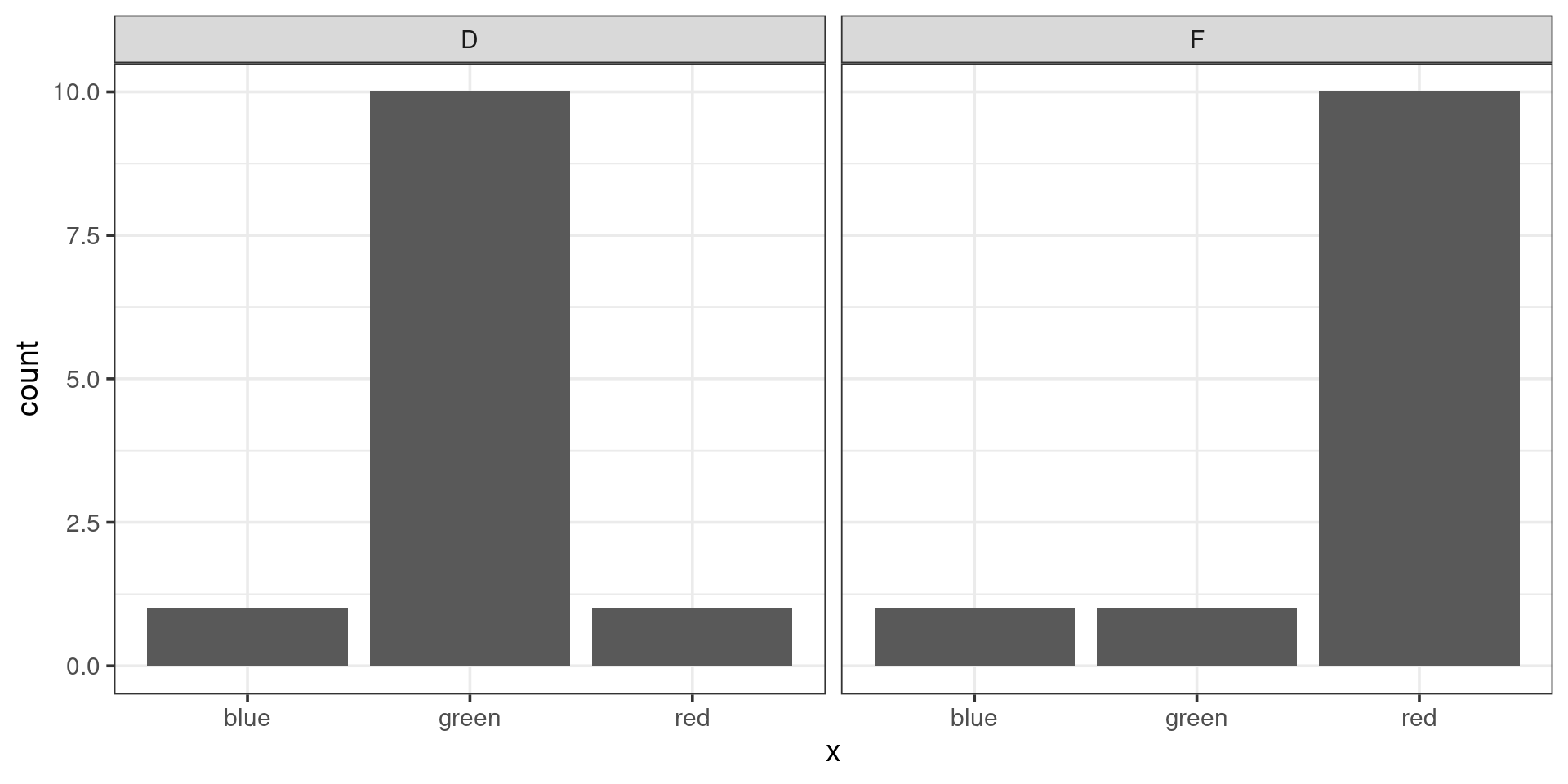
\[ \frac{(1-1)^2}{1} + \frac{(10 - 1)^2}{1} + \frac{(1 - 10)^2}{10} \\ 0 + 81 + \frac{81}{10} = 89.1 \]
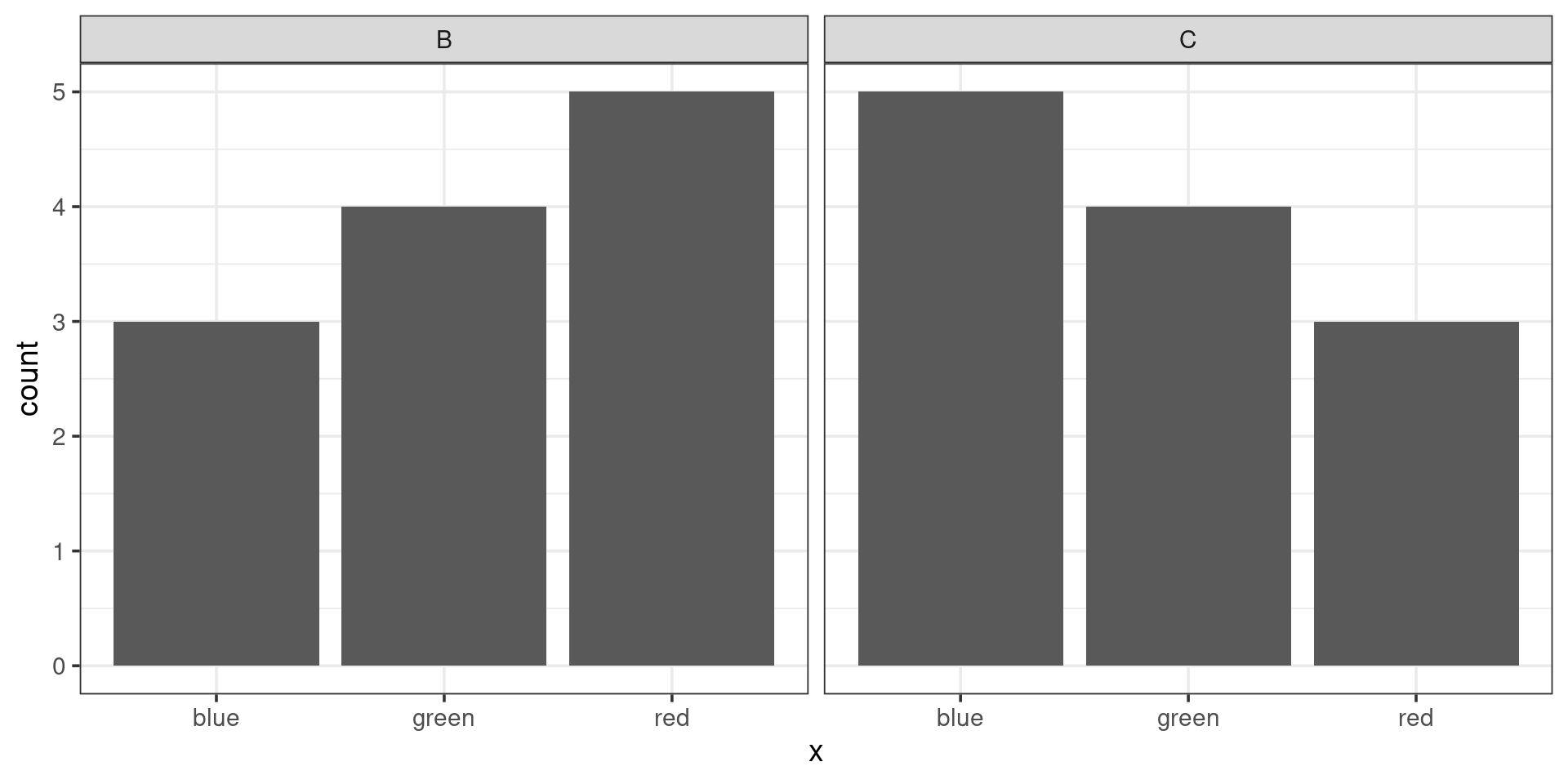
\[ \frac{(3-5)^2}{5} + \frac{(4-4)^2}{4} + \frac{(5-3)^2}{3} \\ \frac{4}{5} + 0 + \frac{4}{3} = 2.13 \]
An In-class Experiment
In order to demonstrate how to conduct a hypothesis test through simulation, we will be collecting data from this class using a poll.
You will have only 15 seconds to answer the following multiple choice question, so please get ready at pollev.com…
The two shapes above have simple first names:
- Booba
- Kiki
Which of the two names belongs to the shape on the left?
00:15
Steps of a Hypothesis Test
- Assert a model for how the data was generated (the null hypothesis)
- Select a test statistic that bears on that null hypothesis (a mean, a proportion, a difference in means, a difference in proportions, etc).
- Approximate the sampling distribution of that statistic under the null hypothesis (aka the null distribution)
- Assess the degree of consistency between that distribution and the test statistic that was actually observed (either visually or by calculating a p-value)
1. The Null Hypothesis
- Let \(p_k\) be the probability that a person selects Kiki for the shape on the left.
- Let \(\hat{p}_k\) be the sample proportion of people that selected Kiki for the shape on the left.
What is a statement of the null hypothesis that corresponds to the notion the link between names and shapes is arbitrary?
01:00
2. Select a test statistic
\[\hat{p}_k = \frac{\textrm{Number who chose "Kiki"}}{\textrm{Total number of people}}\]
Note: you could also simply \(n_k\), the number of people who chose “Kiki”.
3. Approximate the null distribution
Our technique: simulate data from a world in which the null is true, then calculate the test statistic on the simulated data.
Which simulation method(s) align with the null hypothesis and our data collection process?
01:00
Simulating the null using infer
library(tidyverse)
library(infer)
# update these based on the poll
n_k <- 40
n_b <- 20
shapes <- data.frame(name = c(rep("Kiki", n_k),
rep("Booba", n_b)))
shapes |>
specify(response = name,
success = "Kiki") |>
hypothesize(null = "point", p = .5) |>
generate(reps = 1, type = "draw") |>
calculate(stat = "prop")4. Assess the consistency of the data and the null
null <- shapes |>
specify(response = name,
success = "Kiki") |>
hypothesize(null = "point", p = .5) |>
generate(reps = 500, type = "draw") |>
calculate(stat = "prop")
obs_p_hat <- shapes |>
specify(response = name,
success = "Kiki") |>
# hypothesize(null = "point", p = .5) |>
# generate(reps = 500, type = "simulate") |>
calculate(stat = "prop")4. Assess the consistency of the data and the null
The p-value
What is the proper interpretation of this p-value?
01:00
The Bouba / Kiki Effect
Break
05:00
Problem Set 14: Hypothesis Testing II
50:00