Lab 3: Flights

Slides

Part I: Understanding the Context of the Data

For the questions on the handout, consult the image of the data frame found in the slides linked above.

Part II: Computing on the Data

The data for this lab can be found in the flights data frame in the stat20data package. Run ?flights at the console to learn more about the columns.

Question 1

Filter the data set to contain only the flights that left in the springtime destined for Portland, Oregon and print the first few rows of the data frame. How many were there in 2020?

Question 2

Mutate a new variable called avg_speed that is the average speed of the plane during the flight, measured in miles per hour. Save it back into the data frame; you’ll use it later on (Look through the column names or the help file to find variables that can be used to calculate this.)

Question 3

Arrange the data frame to figure out: which flight holds the record for longest departure delay (in hrs) and what was its destination? What was the destination and delay time (in hrs) for the flight that was least delayed, i.e. that left the most ahead of schedule?

Question 4

Confirm the records for departure delay from the question above by summarizing that variable by its maximum and its minimum value.

Question 5

What is the mean departure delay of flights leaving from Oakland and San Francisco separately? (calculate two means)

Question 6

What proportion of the flights left on or ahead of schedule? For Oakland and SFO separately, what proportion of flights left on or ahead of schedule?

Question 7

How many flights left SFO during March 2020? See the examples of Data Pipelines in the Conditioning notes for a helpful function.

Question 8

How many flights left SFO during April 2020?

Question 9

Create a bar chart that shows the distribution by month of all the flights leaving the Bay Area (SFO and OAK). Do you any sign of an effect of the pandemic?

Question 10

Create a histogram showing the distribution of departure delays for all flights. Describe in words the shape and modality of the distribution and, using numerical summaries, (i.e. summary statistics) its center and spread. Be sure to use measures of center and spread that are most appropriate for this type of distribution. Also set the limits of the x-axis to focus on where most of the data lie.

Question 11

Add a new column to your data frame called before_times that takes values of TRUE and FALSE indicating whether the flight took place up through the end of March or after April 1st, respectively. Remake the histograms above, but now separated into two subplots: one with the departure delays from the before times, the other with the flights from afterwards. Can you visually detect any difference in the distribution of departure delays?

This is best done with a new layer called facet_wrap(). Learn about it’s use by reading the documentation: https://ggplot2.tidyverse.org/reference/facet_wrap.html.

Question 12

If you flew out of OAK or SFO during this time period, what is the tail number of the plane that you were on? If you did not fly in this period, find the tail number of the plane that flew JetBlue flight 40 to New York’s JFK Airport from SFO on May 1st.

Question 13

Create a data frame that contains the median and interquartile range for departure delays, grouped by carrier. Which carrier has the lowest typical departure delay? Which one has the least variable departure delays?

Question 14

Create a plot that captures the relationship of average speed vs. distance and describe the shape and structure that you see. What phenomena related to taking flights from the Bay Area might explain this structure?

Question 15

For flights leaving SFO, which month has the highest average departure delay? What about the highest median departure delay? Which of these measures is more useful to know when deciding which month(s) to avoid flying if you particularly dislike flights that are severely delayed?

Question 16

Each individual airplane can be uniquely identified by its tailnumber in the same way that US citizens can be by their social security numbers. Which airplane flew the farthest during this year for which we have data? How many times around the planet does that translate to?

Question 17

What is the tailnumber of the fastest plane in the data set? What type of plane is it (google it!)? Be sure to be clear how you’re defining fastest.

Question 18

Using the airport nearest your hometown, which day of the week and which airline seems best for flying there from San Francisco? If you’re from near SFO or OAK or from abroad, use Chicago as your hometown. Be clear on how you’re defining best.

Note that there is no explicit weekday column in this data set, but there is sufficient information to piece it together. The following line of code can be added to your pipeline to create that new column. It uses functions in the lubridate package, so be sure to load it in at the start of this exercise.

mutate(day_of_week = wday(ymd(paste(year, month, day, set = "-")), label = T))

Question 19

The plot below shows the relationship between the number of flights going out of SFO and the average departure delay. It illustrates the hypothesis that more flights on a given day would lead to a more congested airport which would lead to greater delays on average. Each point represents single day in 2020; there are 366 of them on the plot. Please form a single chain that will create this plot, starting with the raw data set.

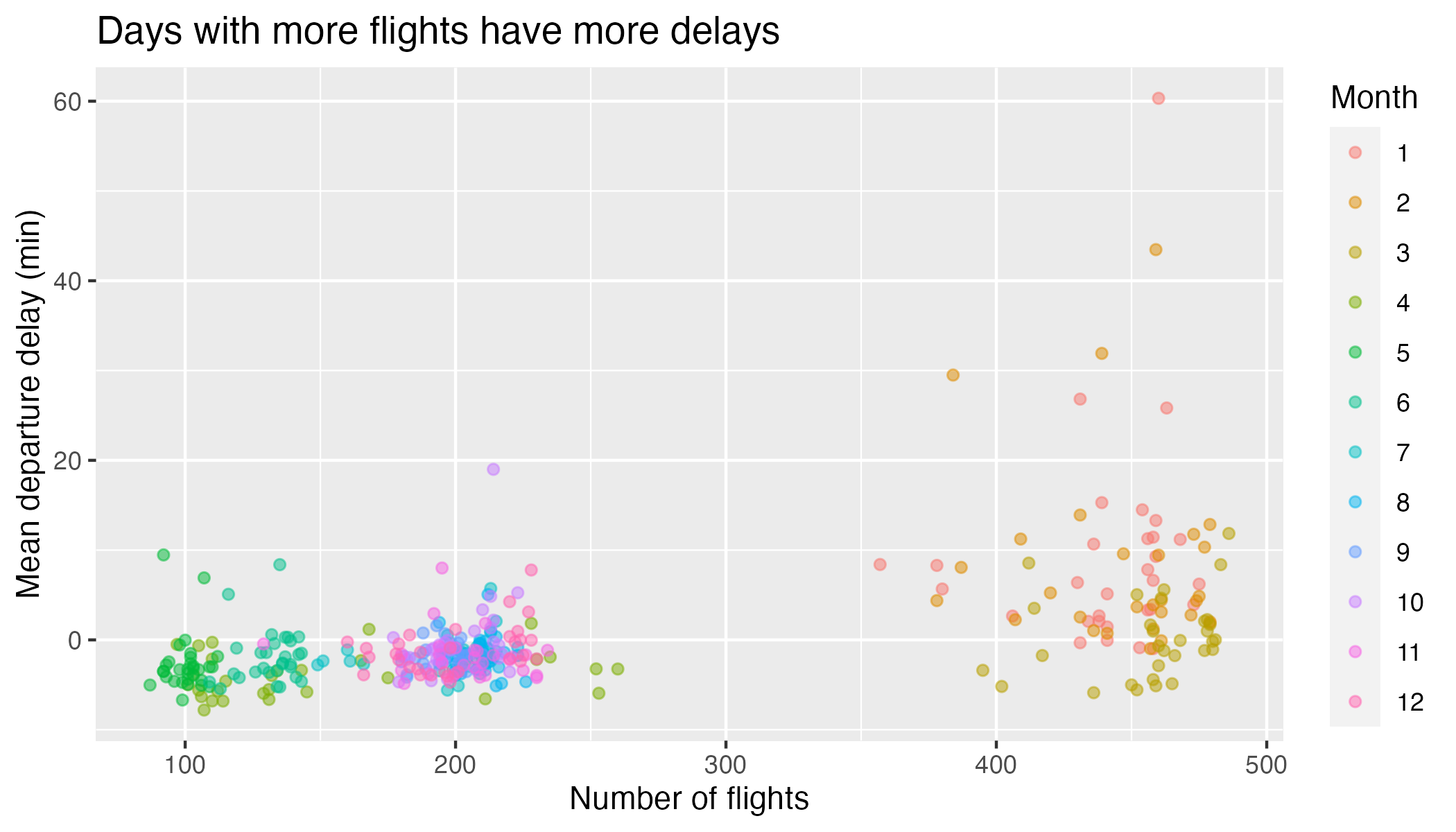
Question 20

Create a plot to illustrate the association between departure delay and arrival delay. Summarize the linear relationship by calculating the correlation coefficient and by fitting a linear model.

Which flight has the highest arrival delay given its departure delay? (Consult the slides from Summarizing Associations for helpful code. For an extra challenge, use the code from the notes to superimpose the linear model on the scatter plot).

Question 21

Fit a multiple linear regression model that explains arrival delay using departure delay and the distance of the flight and print out the coefficients (the intercept and two slopes). Speculate as to why the sign (positive or negative) of the distance coefficient is what it is. Can we compare the coefficients for departure delay and distance to understand which has the stronger relationship? Why or why not?