Conditioning

STAT 20: Introduction to Probability and Statistics

Agenda

Concept Questions
Data Pipelines
Break
Worksheet - Digital
Lab 3.1: Flights

Concept Questions

Question 1

c("fruit", "fruit", "vegetable") == "fruit"

What will this line of code return?

Respond at pollev.com.

01:00

Evaluating equivalence, cont.

In R, this evaluation happens element-wise when operating on vectors.

c("fruit", "fruit", "vegetable") == "fruit"

[1]  TRUE  TRUE FALSE

c("fruit", "fruit", "vegetable") != "fruit"

[1] FALSE FALSE  TRUE

c("fruit", "vegetable", "boba") %in% c("fruit", "vegetable")

[1]  TRUE  TRUE FALSE

Question 2

Which observations will be included in the following data frame?

filter(class_survey, 
       coding_exp_scale < 3,
       olympic_sport %in% c("Ice skating", "Speed skating"),
       entrepreneur == TRUE)

Please respond at pollev.com.

01:00

Question 3: Opinion

What are students’ perceptions of the chance that there is a new COVID variant that disrupts instruction in Spring 2023?

Do you think students in their first semester would be more likely or less likely to think we would remain in remote learning for the entire semester?

Answer at pollev.com.

Question 4

Which data frame will have fewer rows?

class_survey <- mutate(class_survey, 
                       first_sem = year == "This is my first semester!")

# this one
df_1 <- filter(class_survey, first_sem)

# or this one
df_2 <- filter(class_survey, year == "This is my first semester!")

01:00

Building data pipelines

Question 2 Redux

How do we extract the average of these students’ chance that class will be disrupted by a new COVID variant?

filter(class_survey, 
       coding_exp_scale < 3,
       olympic_sport %in% c("Ice skating", "Speed skating"),
       entrepreneur == TRUE)

Question 2 Redux

How do we extract the average of these students’ chance that class will be disrupted by a new COVID variant?

select(filter(class_survey, 
       coding_exp_scale < 3,
       olympic_sport %in% c("Ice skating", "Speed skating"),
       entrepreneur == TRUE),
       coding_exp_xcale,
       olympic_sport,
       entrepreneur,
       new_COVID_variant)

Question 2 Redux

How do we extract the average of these students’ chance that class will be disrupted by a new COVID variant?

summarize(select(filter(class_survey, 
       coding_exp_scale < 3,
       olympic_sport %in% c("Ice skating", "Speed skating"),
       entrepreneur == TRUE),
       coding_exp_scale,
       olympic_sport,
       entrepreneur,
       new_COVID_variant),
       covid_avg = mean(new_COVID_variant))

Question 2 Redux

How do we extract the average of these students’ chance that class will be disrupted by a new COVID variant?

summarize(select(filter(class_survey, 
       coding_exp_scale < 3,
       olympic_sport %in% c("Ice skating", "Speed skating"),
       entrepreneur == TRUE),
       coding_exp_scale,
       olympic_sport,
       entrepreneur,
       new_COVID_variant),
       covid_avg = mean(new_COVID_variant))

# A tibble: 1 × 1
  covid_avg
      <dbl>
1      0.52

Data Pipelines

Most claims about data start with a raw data set, undergo many subsetting, aggregating, and cleaning operations, then return a data product.

Let’s look at three equivalent ways to build a pipeline

Nesting

summarize(select(filter(class_survey, 
       coding_exp_scale < 3,
       olympic_sport %in% c("Ice skating", "Speed skating"),
       entrepreneur == TRUE),
       coding_exp_scale,
       olympic_sport,
       entrepreneur,
       new_COVID_variant),
       covid_avg = mean(new_COVID_variant))

Cons

Must be read from inside out 👎
Hard to keep track of arguments 👎

Pros

All in one line of code 👍
Only refer to one data frame 👍

Step-by-step

df1 <- filter(class_survey, 
              coding_exp_scale < 3,
              olympic_sport %in% c("Ice skating", "Speed skating"),
              entrepreneur == TRUE)
df2 <- select(df1, 
              coding_exp_scale,
              olympic_sport,
              entrepreneur,
              new_COVID_variant)
summarize(df2,
          covid_avg = mean(new_COVID_variant))

Cons

Have to repeat data frame names 👎
Creates unnecessary objects 👎

Pros

Stores intermediate objects 👍
Can be read top to bottom 👍

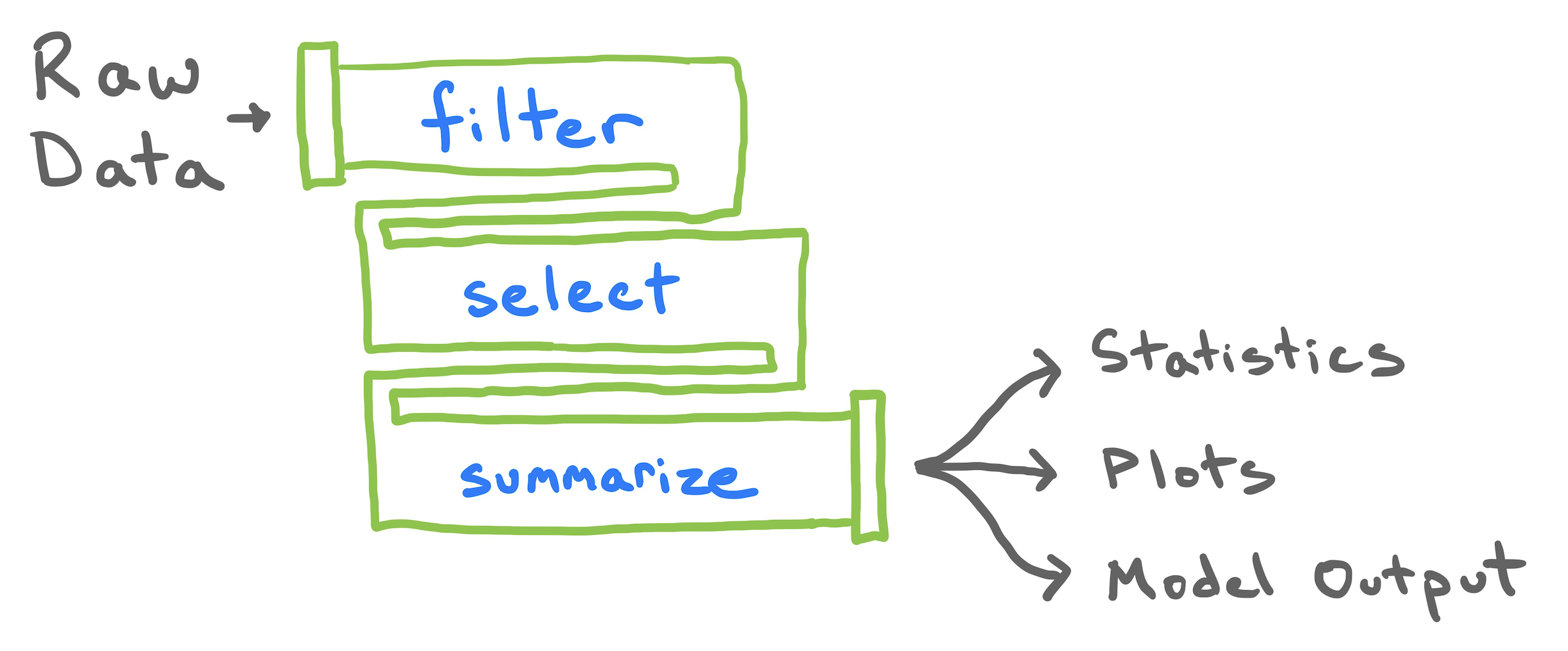
Using the pipe operator

class_survey %>%
  filter(coding_exp_scale < 3,
         olympic_sport %in% c("Ice skating", "Speed skating"),
         entrepreneur == TRUE) %>%
  select(coding_exp_scale,
         olympic_sport,
         entrepreneur,
         new_COVID_variant) %>%
  summarize(covid_avg = mean(new_COVID_variant))

Cons

🤷

Pros

Can be read like an english paragraph 👍
Only type the data once 👍
No leftovers objects 👍

Understanding your pipeline

It’s good practice to understand the output of each line of code by breaking the pipe.

class_survey %>%
  select(new_COVID_variant) %>%
  filter(year == "It's my first year.")

Error in `filter()`:
ℹ In argument: `year == "It's my first year."`.
Caused by error in `year == "It's my first year."`:
! comparison (==) is possible only for atomic and list types

class_survey %>%
  select(new_COVID_variant)

# A tibble: 619 × 1
   new_COVID_variant
               <dbl>
 1           0.25   
 2           0.1    
 3           0      
 4           0.2    
 5           0.9    
 6           0.2    
 7           0.4    
 8           0.00005
 9           0.2    
10           0.3    
# ℹ 609 more rows

Question 5

class_survey %>% # A #<<
  filter(coding_exp_scale < 3,
         olympic_sport %in% c("Ice skating", 
                         "Speed skating"),
         entrepreneur == TRUE) %>% # B #<<
  select(coding_exp_scale,
         olympic_sport,
         entrepreneur,
         new_COVID_variant) %>% # C #<<
  summarize(covid_avg = mean(new_COVID_variant)) # D #<<

What are the dimensions (rows x columns) of the data frames output at each stage of this pipe?

01:00

Question 2: Code

Do you think first year students would be more likely or less likely to think we would remain in remote learning for the entire semester?

Which commands are needed to help answer this question?

class_survey %>%
    filter(year) %>%

Describing `new_COVID_variant`

library(tidyverse)
library(stat20data)
class_survey <- class_survey %>%
  select(year, new_COVID_variant) %>%
  mutate(new_COVID_variant = round(new_COVID_variant, digits = 2))

ggplot(class_survey, aes(x = new_COVID_variant)) +
  geom_histogram()

Aside: density plot

ggplot(class_survey, aes(x = new_COVID_variant)) +
  geom_density() #<<

Describing `new_COVID_variant`

ggplot(class_survey, aes(x = new_COVID_variant)) +
  geom_histogram()

summarize(class_survey,
          mean = mean(new_COVID_variant),
          med = median(new_COVID_variant),
          iqr = IQR(new_COVID_variant),
          sd = sd(new_COVID_variant))

# A tibble: 1 × 4
   mean   med   iqr    sd
  <dbl> <dbl> <dbl> <dbl>
1 0.368   0.3  0.35 0.468

The distribution of probabilities of all students is right-skewed with a mean probability of 0.37 and a median probability of 0.3, an IQR of 0.35 and a SD of 0.47.

Describing first year students

How can we focus our analysis on just first year students?

General goal: Identify whether the value in a variable meets a condition.

Here: Is the value in new_COVID_variant equal to "I'm in my first year."?

Our Tool, Comparison operators: A collection of operators that compare two values / vectors and return TRUE or FALSE.

Evaluating equivalence

"fruit" == "vegetable"

[1] FALSE

"fruit" == "fruit"

[1] TRUE

"fruit" != "fruit"

[1] FALSE

== evaluates equality, != evaluates inequality.

Adding a grouping variable

class_survey <- mutate(class_survey,
                       first_year = year == "I'm in my first year.")
class_survey

# A tibble: 619 × 3
   year                       new_COVID_variant first_year
   <chr>                                  <dbl> <lgl>     
 1 I'm in my second year.                  0.25 FALSE     
 2 This is my first semester!              0.1  FALSE     
 3 This is my first semester!              0    FALSE     
 4 I'm in my second year.                  0.2  FALSE     
 5 I'm in my first year.                   0.9  TRUE      
 6 I'm in my second year.                  0.2  FALSE     
 7 I'm in my second year.                  0.4  FALSE     
 8 I'm in my second year.                  0    FALSE     
 9 I'm in my second year.                  0.2  FALSE     
10 I'm in my first year.                   0.3  TRUE      
# ℹ 609 more rows

Filtering data using logical vectors

Filtering rows

first_yr_df <- filter(class_survey, first_year)
first_yr_df

# A tibble: 245 × 3
   year                  new_COVID_variant first_year
   <chr>                             <dbl> <lgl>     
 1 I'm in my first year.               0.9 TRUE      
 2 I'm in my first year.               0.3 TRUE      
 3 I'm in my first year.               0.6 TRUE      
 4 I'm in my first year.               0.3 TRUE      
 5 I'm in my first year.               0.3 TRUE      
 6 I'm in my first year.               0.1 TRUE      
 7 I'm in my first year.               0.7 TRUE      
 8 I'm in my first year.               0.2 TRUE      
 9 I'm in my first year.               0.5 TRUE      
10 I'm in my first year.               0.5 TRUE      
# ℹ 235 more rows

Describing `new_COVID_variant` with statistics

Statistics from all students

summarize(class_survey,
          mean = mean(new_COVID_variant),
          med = median(new_COVID_variant),
          iqr = IQR(new_COVID_variant),
          sd = sd(new_COVID_variant))

# A tibble: 1 × 4
   mean   med   iqr    sd
  <dbl> <dbl> <dbl> <dbl>
1 0.368   0.3  0.35 0.468

Statistics from first year students

summarize(first_yr_df,
          mean = mean(new_COVID_variant),
          med = median(new_COVID_variant),
          iqr = IQR(new_COVID_variant),
          sd = sd(new_COVID_variant))

# A tibble: 1 × 4
   mean   med   iqr    sd
  <dbl> <dbl> <dbl> <dbl>
1 0.398   0.3   0.3 0.561

Describing `new_COVID_variant` with graphics

Histogram for all students

ggplot(class_survey, aes(x = new_COVID_variant)) +
  geom_histogram()

Histograms from first year and non-first year students

ggplot(class_survey, aes(x = new_COVID_variant)) +
  geom_histogram() +
  facet_wrap(vars(first_year))

Example 1

What is the mean probability of new_COVID_variant for students who were very confident that we could engineer our way out of the effects of climate change (6 or above on climate_change)?

class_survey

# A tibble: 619 × 3
   year                       new_COVID_variant first_year
   <chr>                                  <dbl> <lgl>     
 1 I'm in my second year.                  0.25 FALSE     
 2 This is my first semester!              0.1  FALSE     
 3 This is my first semester!              0    FALSE     
 4 I'm in my second year.                  0.2  FALSE     
 5 I'm in my first year.                   0.9  TRUE      
 6 I'm in my second year.                  0.2  FALSE     
 7 I'm in my second year.                  0.4  FALSE     
 8 I'm in my second year.                  0    FALSE     
 9 I'm in my second year.                  0.2  FALSE     
10 I'm in my first year.                   0.3  TRUE      
# ℹ 609 more rows

optimist_df <- filter(class_survey, climate_change >= 6)
summarize(optimist_df, mean(new_COVID_variant))

summarize(class_survey, mean(new_COVID_variant))

# A tibble: 1 × 1
  `mean(new_COVID_variant)`
                      <dbl>
1                     0.368

Example 2

What is the mean probability of new_COVID_variant for first-year students who were very confident that we could engineer our way out of the effects of climate change (6 or above on climate_change)?

data("class_survey")

optimist_df <- filter(class_survey,
                      climate_change >= 6,
                      year == "I'm in my first year.")
summarize(optimist_df, mean(new_COVID_variant))

# A tibble: 1 × 1
  `mean(new_COVID_variant)`
                      <dbl>
1                     0.370

> You can string together conditions by adding them as arguments to `filter()` separated by commas.

What else can logical vectors be used for?

summarize(class_survey, mean(year == "I'm in my first year."))

What is will this line of code return?

Respond at pollev.com.

Boolean Algebra

Logical vectors have a dual representation as TRUE FALSE and 1, 0, so you can do math on logicals accordingly.

TRUE + TRUE

[1] 2

TRUE * TRUE

[1] 1

Taking the mean of a logical vector is equivalent to find the proportion of rows that are TRUE (i.e. the proportion of rows that meet the condition).

Break

Worksheet - Digital

25:00

Conditioning

Agenda

Concept Questions

Question 1

Evaluating equivalence, cont.

Question 2

Question 3: Opinion

Question 4

Building data pipelines

Question 2 Redux

Question 2 Redux

Question 2 Redux

Question 2 Redux

Data Pipelines

Nesting

Step-by-step

Using the pipe operator

Understanding your pipeline

Question 5

Question 2: Code

Describing new_COVID_variant

Describing new_COVID_variant

Describing first year students

Evaluating equivalence

Adding a grouping variable

Filtering data using logical vectors

Filtering rows

Describing new_COVID_variant with statistics

Describing new_COVID_variant with graphics

Example 1

Example 2

> You can string together conditions by adding them as arguments to filter() separated by commas.

Boolean Algebra

Break

Worksheet - Digital

Describing `new_COVID_variant`

Describing `new_COVID_variant`

Describing `new_COVID_variant` with statistics

Describing `new_COVID_variant` with graphics

> You can string together conditions by adding them as arguments to `filter()` separated by commas.