Summarizing Numerical Data

STAT 20: Introduction to Probability and Statistics

Agenda

  • Quiz Review
  • Lab 1 Review
  • Concept Question
  • Break
  • Measures of Center
  • Measures of Spread
  • Summarize
  • Break
  • Problem Set 2.1

Quiz Review

Lab 1 Review

Concept Question

Describing Shape

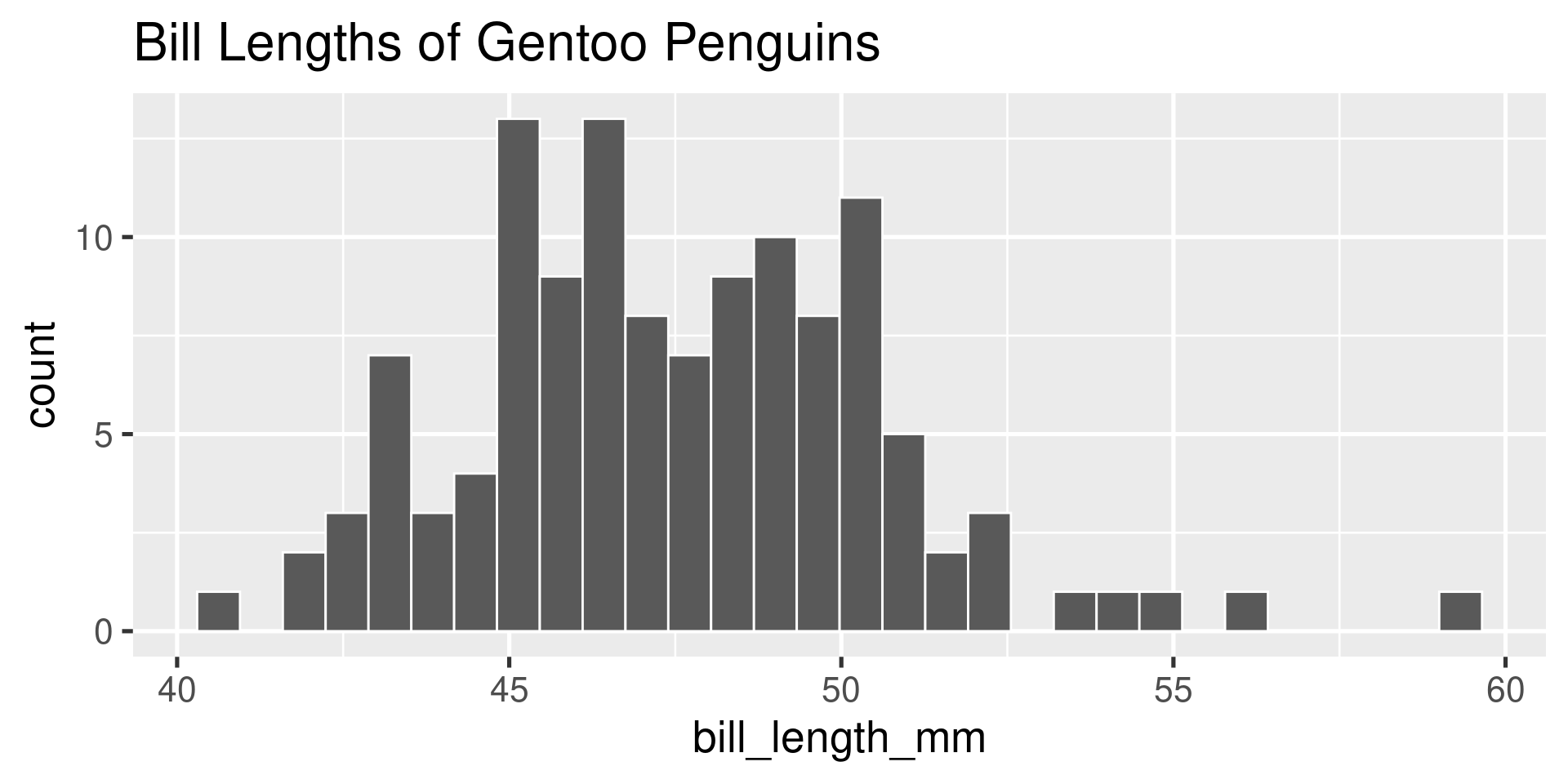
Which of these variables do you expect to be uniformly distributed?

  1. bill length of Gentoo penguins
  2. salaries of a random sample of people from California
  3. house sale prices in San Francisco
  4. birthdays of classmates (day of the month)

Please vote at pollev.com.

01:00

Measures of Center

Mean, median, mode: which is best?

It depends on your desiderata: the nature of your data and what you seek to capture in your summary.

Get out a piece of paper. You’ll be watching a 3 minute video that discusses characteristics of a typical human. Note which numerical summaries are used and what for.

General Advice

  1. Means are often a good default for symmetric data.
  1. Means are sensitive to very large and small values, so can be deceptive on skewed data. > Use a median
  1. Modes are often the only option for categorical data.

But there are other notions of typical…

Measures of Spread

There are two new food delivery services that open in Berkeley: Oski Eats and Cal Cravings. A friend of yours that took Stat 20 collected data on each and noted that Oski Eats has a mean delivery time of 29 minutes and Cal Cravings a mean delivery time of 27 minutes. Which would would you rather order from?

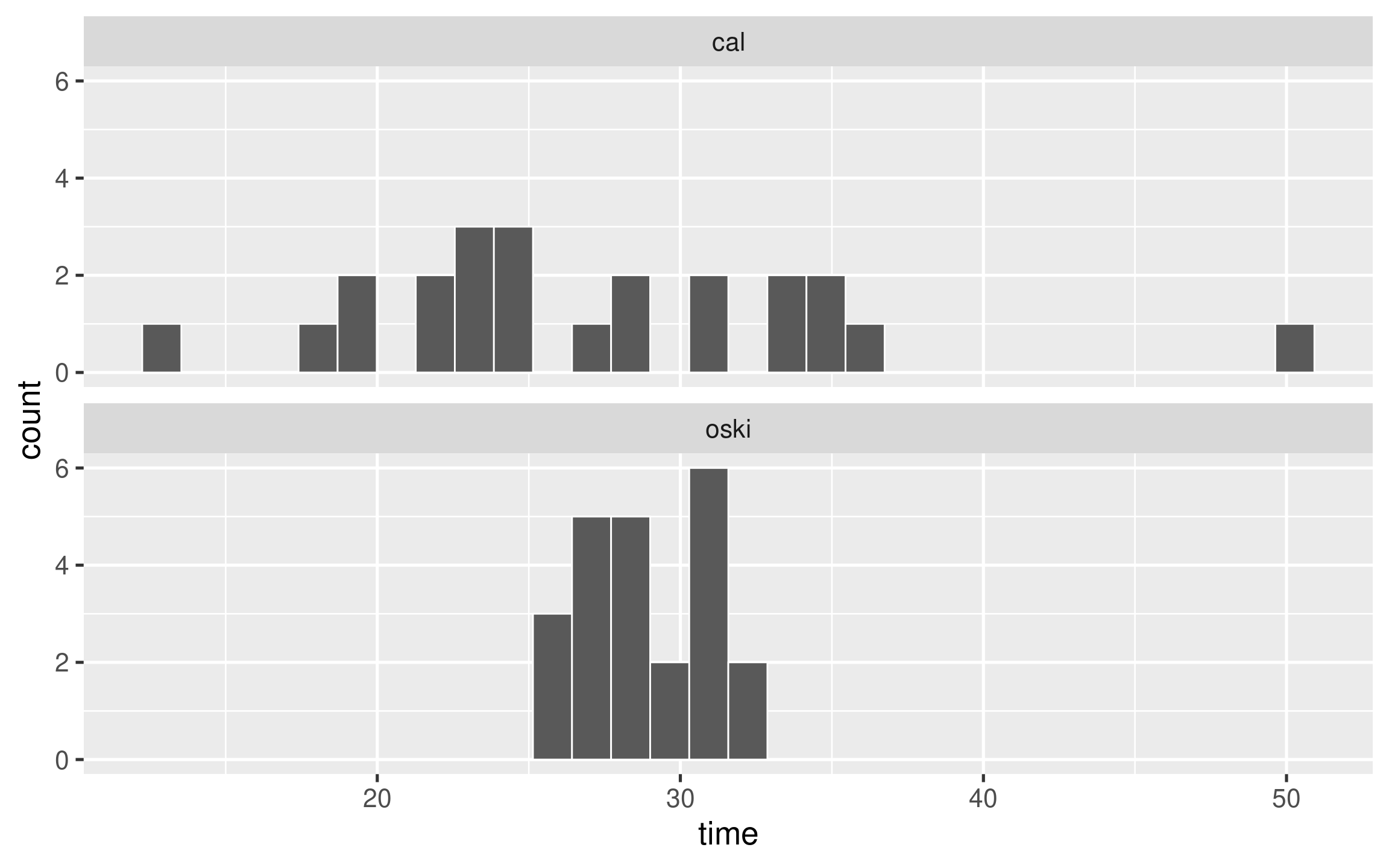
Would you still prefer to order from Cal?

Summarizing Distributions of Data

You can construct a statistical graphic to show the shape, which you can describe in terms of modality and skew… you can calculate a measure of center to convey a sense of a typical observation…and you can calculate a measure of spread to capture how much variability there is in the data.

Statistics as Engineering

We construct tools (statistics, graphics) that produce useful summaries of raw data.

How can we express the variability in this data set using a single number?

\[ 6 \quad 7 \quad 7 \quad 7 \quad 8 \quad 8 \quad 9 \quad 9 \quad 10 \quad 11 \quad 11\]

Desiderata

  • The statistic should be low when the numbers are the same or very similar to one another.
  • The statistic should be high when the numbers are very different.
  • The statistic should not grow or shrink with the sample size ( \(n\) ).

Existing statistics to utilize:

  • sample size ( \(n\) ): 11
  • sample mean ( \(\bar{x}\) ): 8.45
  • sample median: 8
  • sample mode: 7

\[ {\Large 6} \quad 7 \quad 7 \quad 7 \quad 8 \quad 8 \quad 9 \quad 9 \quad 10 \quad 11 \quad {\Large 11}\]

The Range

\[\textrm{range:} \quad max - min\]

\[ 11 - 6 = 5\]

Characteristics

  • Very sensitive to extreme values!

\[ 6 \quad 7 \quad {\Large 7 \quad 7} \quad 8 \quad {\large 8} \quad 9 \quad {\Large 9 \quad 10} \quad 11 \quad 11\]

The Inner Quartile Range (IQR)

The difference between the median of the larger half of the sorted data set, \(Q_3\), and the median of the smaller half, \(Q_1\).

\[\textrm{IQR:} \quad Q_3 - Q_1\]

\[ 9.5 - 7 = 2.5 \]

Characteristics

  • Robust to outliers
  • Used to set the width of the box in a boxplot

\[ 6 \quad 7 \quad 7 \quad 7 \quad 8 \quad 8 \quad 9 \quad 9 \quad 10 \quad 11 \quad 11\]

Mean Absolute Deviation

Take the differences from each observation, \(x_i\), to the sample mean, \(\bar{x}\), take their absolute values, add them up, and divide by \(n\) .

\[MAD: \quad \frac{1}{n}\sum_{i = 1}^n |x_i - \bar{x}| \]

\[ MAD = 1.4 \]

Characteristics

  • Incorporates information from all observations
  • Robust to extreme values

\[ 6 \quad 7 \quad 7 \quad 7 \quad 8 \quad 8 \quad 9 \quad 9 \quad 10 \quad 11 \quad 11\]

Sample Variance

Take the differences from each observation, \(x_i\), to the sample mean, \(\bar{x}\), square them, add them up, and divide by \(n - 1\) .

\[s^2: \quad \frac{1}{n - 1}\sum_{i = 1}^n (x_i - \bar{x})^2 \]

\[ s^2 = 2.87 \]

Characteristics

  • Incorporates information from all observations
  • Moderately sensitive to extreme values

\[ 6 \quad 7 \quad 7 \quad 7 \quad 8 \quad 8 \quad 9 \quad 9 \quad 10 \quad 11 \quad 11\]

Sample Standard Deviation

Take the differences from each observation, \(x_i\), to the sample mean, \(\bar{x}\), square them, add them up, divide by \(n - 1\), then take the square root.

\[s: \quad \sqrt{\frac{1}{n - 1}\sum_{i = 1}^n (x_i - \bar{x})^2} \]

\[ s = 1.70 \]

Characteristics

  • Incorporates info from all observations
  • Moderately sensitive to extreme values
  • Measured in units of the original data

Deliveries revisited

service range IQR var sd
cal 37.4 9.9 62.9 7.9
oski 6.5 3.9 4.3 2.1

Desiderata

  • The statistic should be low when the numbers are the same or very similar to one another.
  • The statistic should be high when the numbers are very different.
  • The statistic should not grow or shrink with the sample size ( \(n\) ).